Анализ чувствительности моделей с помощью VisualAivika

Автор: Давид Сорокин

Дата публикации: 3 августа 2025 года, изменено: 12 августа 2025 года

В этой статье я собираюсь описать, как можно проводить анализ чувствительности имитационных моделей с помощью разработанной мною программы VisualAivika. Речь пойдет о динамических системах, где используются обыкновенные дифференциальные уравнения (ОДУ). Помимо этого, программа поддерживает моделирование систем массового обслуживания (СМО) в рамках дискретно-событийного моделирования. Для приведенной ниже одной системы ОДУ будет использована так называемая диаграмма потоков и накопителей, что является неотъемлемой частью системной динамики. Обе названные парадигмы, системная динамика и дискретно-событийное моделирование, поддерживаются средой визуального моделирования VisualAivika, которую можно скачать с моего сайта по приведенной выше ссылке.

Итак, возьмем модель рыночных долей компаний. Эта модель описана в книге «Business Dynamics» за авторством John D. Sterman, в разделе 10.8.1.

Готовый файл модели можно скачать по следующей ссылке.

Для начала возьмем две фирмы, условно фирма «1» и фирма «2». Моделируем установленную базу для некоторого продукта (Installed Base Product), которая увеличивается вместе с продажами продукта (Sales of Product). Для простоты исключим другие факторы и будем считать, что установленный базовый продукт растет со скоростью продаж продукта, то есть, продажи продукта — это производная для интеграла.

Installed_Base_Product_1 = integ(Sales_of_Product_1, 
    Initial_Installed_Base_of_Product_1);

В VisualAivika ключевое слово integ возвращает интеграл по заданной производной и заданному начальному значению. Аналогичное уравнение будет и для фирмы «2».

Считаем, что продажи продукта пропорциональны доле рынка и зависят от общего спроса:

Sales_of_Product_1 = Total_Demand * Market_Share_Product_1;

Такие отношения между временными рядами можно схематически изобразить на диаграмме следующим образом, как показано на рисунке 1.

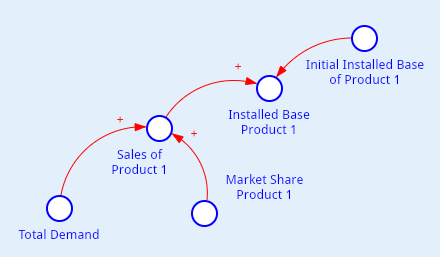
Обратите внимание на знаки «плюсов» рядом со стрелками. Это говорит о том, что такая связь усиливающая. Знак «минус» означал бы ослабляющую связь. В стационарной модели знаки «плюсов» и «минусов» должны быть сбалансированы. Здесь модель неполная — поэтому мы этого пока не видим.

На самом деле, для приведенной модели в системной динамике принято использовать более специализированные диаграммы потоков и накопителей. Та же самая модель будет выглядеть так, как показано на рисунке 2.

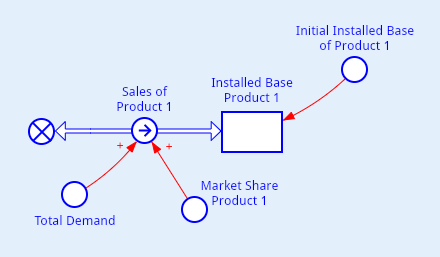
Теперь здесь интеграл (Installed_Base_Product_1) будет называться накопителем, а его производная — потоком (Sales_of_Product_1).

А так, это та же самая система ОДУ. Просто, накопители бывает еще разные. Интеграл иногда называют накопителем резервуара. Преимуществом таких диаграмм является то, что сразу видно интегралы и производные. Впрочем, в VisualAivika интегралы можно использовать и как обычные функции в математических выражениях.

Здесь и далее используем длинные названия переменных, потому что так принято в системной динамике. Другой причиной является то, что так удобнее работать с диаграммой. А что касается написания уравнений, то в VisualAivika подстановка длинных названий переменных в уравнения автоматизирована.

Когда мы соединяем стрелками сущности диаграммы, то VisualAivika запоминает, что от чего должно зависеть. Если вы напишите уравнение, которое не будет соответствовать диаграмме, то VisualAivika высветит предупреждение. В то же время, в редакторе уравнений появится список, по которому в редактируемое математическое выражение можно вставить название переменной по одному лишь щелчку мышки. Редактор уравнений показан на рисунке 3.

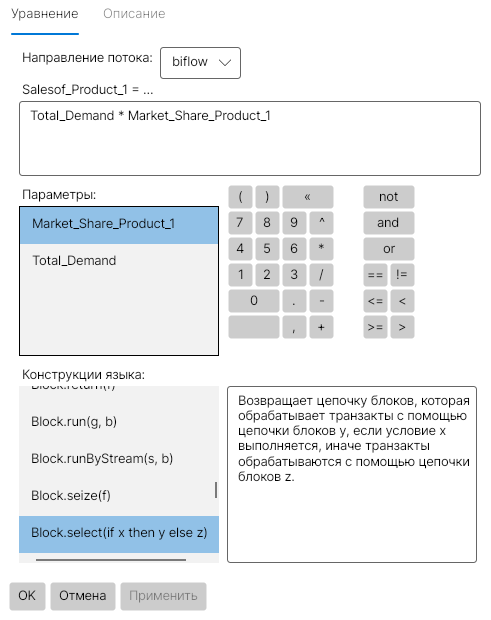
Вернемся к нашей модели. Будем считать, что рыночная доля определяется привлекательностью продукта и нормируется по общей привлекательности всех продуктов, которые представлены на рынке.

Market_Share_Product_1 = 
    Attractiveness_of_Product_1 / 
        Total_Attractiveness_of_All_Products;

Тогда общая привлекательность всех продуктов определяется как сумма.

Total_Attractiveness_of_All_Products = 
    Attractiveness_of_Product_1 + 
        Attractiveness_of_Product_2;

Когда мы обобщим эту модель на случай нескольких фирм, то здесь появится функция агрегирования по массиву. Пока же имейте в виду, что это единственная формула, где идет агрегирование, а остальные формулы зеркальны для каждой из фирм.

Привлекательность продукта оценим как произведение двух факторов: эффекта от совместимости (сетевой эффект) и эффекта от других случайных факторов.

Attractiveness_of_Product_1 = 
    Effect_of_Compatibility_on_Attractiveness_of_Product_1 * 
        Effect_of_Other_Factors_on_Attractiveness_of_Product_1;

В упоминаемой книге приводится такой пример. Что если у нас всего два телефонных аппарата на всю страну, то эффект от обладания третьим аппаратом довольно низкий. Тогда как, если в стране уже есть 100 миллионов телефонных аппаратов, то эффект от привлекательности гораздо выше. Это сетевой эффект.

Считаем, что эффект от совместимости изменяется экспоненциально.

Effect_of_Compatibility_on_Attractiveness_of_Product_1 = 
    exp(Sensitivity_of_Attractiveness_to_Installed_Base * 
            (Installed_Base_of_Product_1 / 
                 Threshold_for_Compatibility_Effects));

Мы здесь делим на некоторое пороговое значение, которое можно интерпретировать следующим образом. Чтобы эффект возымел свое действие, должна набраться некоторая критическая масса по установленной базе.

Что касается эффекта от случайных факторов, то считаем, что в точках интегрирования ОДУ этот эффект подчиняется нормальному распределению со средним 1 и некоторым отклонением, задаваемым как внешний параметр. Среднее значение 1 нужно, потому что мы умножаем два эффекта.

Effect_of_Other_Factors_on_Attractiveness_of_Product_1 = 
    normal(1, Standard_Deviation_of_Random_Effects_on_Attractiveness);

Считаем, что форма закона распределения общая для обеих компаний, но эффект для каждой компании будет свой. То есть, случайные процессы будут разными для обеих компаний.

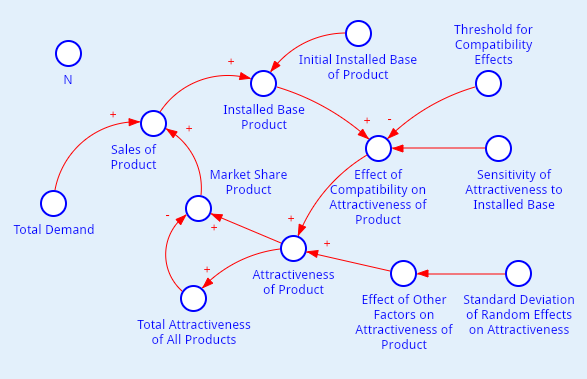
Таким образом, мы построили стохастическую систему ОДУ, которая зависит от нескольких внешних параметров. В этой модели пока количество компаний равно двум. Схематическое изображение соответствующей диаграммы потоков и накопителей приведено на рисунке 4.

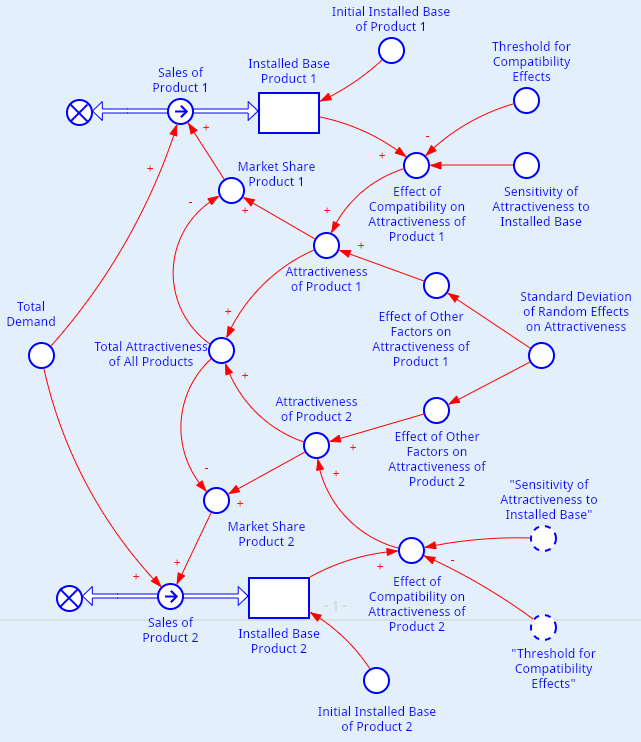
Здесь пунктирными линиями изображены элементы, которые ссылаются на уже существующие элементы диаграммы. Это необходимо для того, чтобы диаграмму сделать более простой.

Также обратите особое внимание на то, что здесь есть связи со знаком «минус». Они балансируют поведение модели.

Нам осталось доопределить некоторые параметры модели. Возьмем те же значения, что указаны в книге «Business Dynamics» в таблице 10-2.

Total_Demand = 1;   // миллионов единиц в год
Sensitivity_of_Attractiveness_to_Installed_Base = 2;
Threshold_for_Compatibility_Effects = 1;    // миллионов единиц
Standard_Deviation_of_Random_Effects_on_Attractiveness = 0.01;

Считаем, что начальная установленная база для каждой из фирм равна 1, то есть, считаем, что обе фирмы стартовали с равных условий.

Initial_Installed_Base_of_Product_1 = 1;
Initial_Installed_Base_of_Product_2 = 1;

Пусть конечное время моделирования будет равно 10 годам, а шаг интегрирования равен 0,25 года. Зададим эксперимент по методу Монте-Карло с общим количеством запусков 2000.

На графиках выведем рыночную долю обеих компаний, сначала в виде простых временных рядов для разных имитационных запусков. Это будут случайные процессы. Их траектории будут отличаться от запуска к запуску. Изображения двух графиков с некоторыми случайными траекториями изображены на рисунках 5 и 6, соответственно.

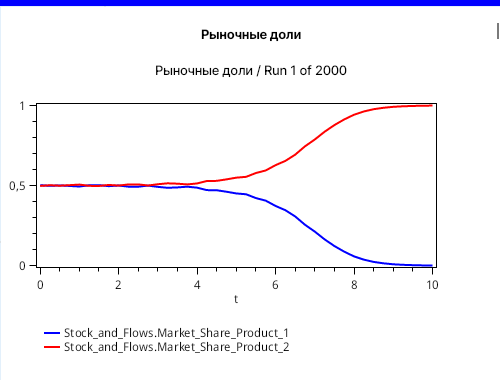
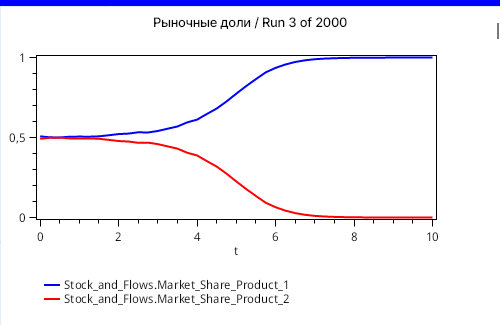
На обоих графиках мы видим, что любая фирма в рамках этой упрощенной модели может захватить весь рынок. Все определяется случайным фактором — там, где мы использовали случайный процесс из независимых нормально распределенных величин.

На самом деле, случайные параметры могут быть и постоянными в рамках одного запуска, но потом их значение может поменяться для другого запуска. Это открывает путь к планированию эксперимента в VisualAivika. Для демонстрации мы пока ограничимся введенной случайностью через использованную функцию normal.

Мы можем агрегировать информацию обо всех 2000-х запусков сразу на одном графике. Так, если мы выведем график отклонения для рыночной доли первой компании, то тогда получим изображение тренда и доверительных интервалов по правилу 3-сигм, как изображено на рисунке 7.

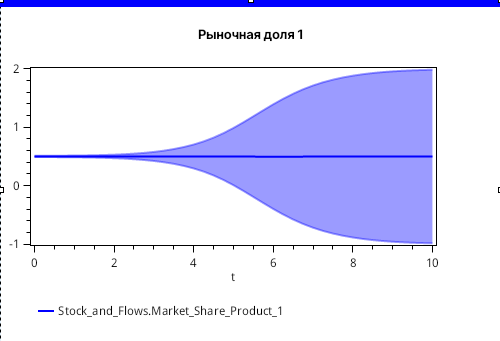
В среднем получается, что рыночная доля стремится к значению 0,5. Это соответствует значению в 50%, но график тренда обманчив. Это всего лишь среднее значение по всем имитационным запускам.

Мы увидим реальное положение дел, если выведем гистограммы рыночных долей обеих фирм в конечной точке моделирования, как показано на рисунке 8.

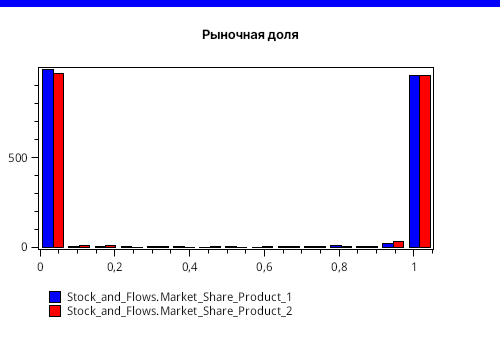
Здесь картина не совсем такая радужная. Интерпретируя все три вида графиков вместе, мы видим, что одна из фирм через 10 лет забирает все, а другая теряет весь рынок. И лишь некоторый шум на графиках говорит, что так происходит не всегда, но почти всегда.

А вот, если сократить конечное время моделирование до 6 лет, то тогда можно увидеть еще острую конкурентную борьбу между обеими фирмами. Это иллюстрирует гистограмма, изображенная на рисунке 9.

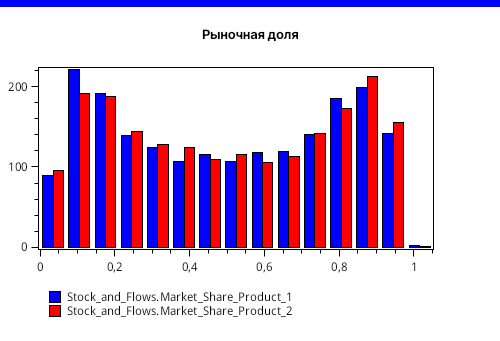
Здесь, конечно, нужно понимать, что это всего лишь имитационная модель, которая многое упрощает. Поэтому интерпретировать такие результаты всегда нужно осторожно.

Наконец, в VisualAivika можно вывести сводную статистику по показателю рыночной доли для обеих фирм. Это показано на рисунке 10.

Здесь особое значение имеют экстремумы. Мы видим, что рыночные доли ограничены в интервале от 0% до 100%, что соответствует нашим ожиданиям.

Меняя значения внешних параметров, можно посмотреть, как поведет себя модель при новых условиях. В этом и будет состоять анализ чувствительности, а вспомогательные графики, которые мы видели, помогут интерпретировать результаты.

Для вводной статьи приведено уже достаточно много информации. В дополнение скажу, что эту модель можно обобщить на случай нескольких фирм, используя массивы. Только нам придется отказаться от использования потоков и накопителей, но сама диаграмма останется.

Итак, введем новую переменную N для обозначения количества фирм. Также избавимся от окончаний «1» и «2». Будем использовать массивы. Все уравнения показывать не стану. Покажу лишь основные моменты.

Установочная база для продуктов превращается в массив интегралов, где индекс меняется от 1 до N.

Installed_Base_Product = 
    [ integ(Sales_of_Product[i], 
            Initial_Installed_Base_of_Product[i]) | i <- 1..N ];

Эта запись, по сути, является генератором массива. Она похожа на то, как можно создавать массивы и списки в таких языках как Haskell, F#, Python и Erlang. Идея та же. В VisualAivika это основной способ для создания массивов.

Похожим образом создаем производные для таких интегралов, тоже в виде массива.

Sales_of_Product = 
    [ Total_Demand * Market_Share_Product[i] | i <- 1..N ];

Аналогичным образом меняются и другие уравнения за исключением агрегирования. Здесь мы просто вызываем встроенную функцию, которая посчитает сумму значений вектора.

Total_Attractiveness_of_All_Products = sum(Attractiveness_of_Product);

В итоге у нас получится даже более простая диаграмма модели, которая изображена на рисунке 11.

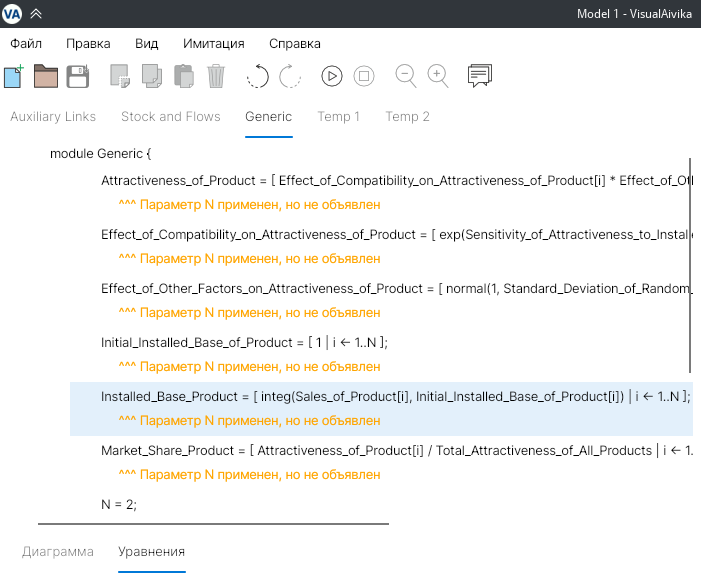
Стоит заметить, что хотя здесь массивы теперь зависят от переменной N, эта связь явно не отображена на диаграмме. По этой причине панель уравнений VisualAivika создает множество предупреждений о несоответствии уравнений и диаграммы, но это нисколько не мешает самому моделированию. Эти предупреждения на панели уравнений выглядят так, как показано на рисунке 12.

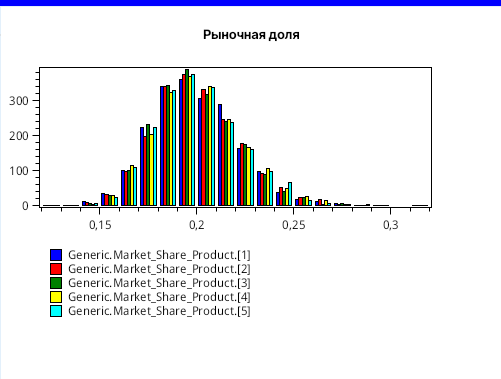
И когда я задал количество фирм равным 5 (N = 5), то получил довольно интересное распределение рыночных долей для модельного времени в 10 лет. Результат изображен на рисунке 13.

Если захотите тоже что-нибудь промоделировать с помощью VisualAivika, то имейте в виду, что массивы гораздо быстрее обсчитывает та версия, где используется компилятор уравнений. В такой версии по имитационной модели создается код на C#. Поэтому такой версии нужно, чтобы был установлен .NET. Другая же версия с интерпретатором уравнений может работать без установленного .NET.

А так, вполне может быть любопытным узнать то, как распределятся рыночные доли пяти компаний, скажем, через 20 лет? Как распределятся доли, если компании стартовали из разных условий? А если пороги привлекательности продуктов менялись со временем, или они были разными для разных запусков и зависели случайно? На эти и подобные вопросы может ответить анализ чувствительности. Да и саму модель можно доработать.

Например, чтобы внешний параметр чувствительности к сетевому эффекту был случайным для разных запусков, но постоянным в рамках текущего запуска, то можно использовать дополнительные случайные функции, такие как показано в уравнении ниже.

Sensitivity_of_Attractiveness_to_Installed_Base = randomParam(1.9, 2.1);

Здесь внешний параметр будет постоянным в рамках каждого имитационного запуска, но при этом он будет случайным с равномерным распределением в интервале между 1,9 и 2,1.

Я надеюсь, что вам было интересно познакомиться с программой VisualAivika, которую я разработал. Напоследок напишу, что VisualAivika поддерживает и вычисления блоков, которые похожи на язык моделирования GPSS. Такие блоки можно использовать для моделирования систем СМО массового обслуживания и сетей очередей. Более того, системы ОДУ и системы СМО можно комбинировать в рамках одной модели, но это все — темы для других статей.