Моделирование замкнутой сети очередей в VisualAivika

Автор: Давид Сорокин

Дата публикации: 11 августа 2025 года, изменено: 12 августа 2025 года

В этой статье я собираюсь описать, как можно с помощью разработанной мною программы VisualAivika моделировать системы массового обслуживания (СМО), используя массивы. Помимо этого, программа поддерживает системы обыкновенных дифференциальных уравнений (ОДУ), но здесь пойдет речь об одной известной задаче из дискретно-событийного моделирования.

Итак, задача заключается в моделировании замкнутой сети очередей. Например, она описана в статье “Performance evaluation of conservative algorithms in parallel simulation languages” (2000) за авторством R. L. Bagrodia и M. Takai, а также в статье “Parallel simulation made easy with OMNeT++” (2003) за авторством Varga, A., Sekercioglu, A.Y. Я тоже часто ссылался на эту задачу в своих работах, но мы ниже увидим, что сама постановка может несколько отличаться в некоторых мелких деталях.

У нас есть N тандемов очередей. В каждом тандеме находится k серверов, соединенных друг за другом. Каждый сервер обрабатывает заявку, пусть показательно со средним 10 единиц модельного времени, а потом с некоторой задержкой передает заявку следующему серверу в тандеме. Пусть задержка равна 1 единице времени. Когда дело доходит до последнего сервера в тандеме, то такой сервер по окончании обработки передает заявку случайным образом первому серверу одного из тандемов. Пусть тандем выбирается равномерно, причем при пересылке заявки случайно выбранному тандему прибавляется еще дополнительная задержка, которая определяется параметром предсказания, что указывает на связь этой задачи с параллельным и распределенным дискретно-событийным моделированием. Пусть эта задержка равна 100 единицам времени. Наконец, заявки создаются только в начале имитации, пусть по 60 заявок на 1 тандем, а затем заявки начинают циркулировать внутри системы из тандемов очередей. Требуется определить количество заявок, обработанных тандемами. Для начала положим, что тандемов четыре (N = 4), а серверов - пятьдесят (k = 50).

На рисунке 1 схематически изображена такая модель замкнутой сети очередей.

Мы сейчас решим эту задачу с помощью VisualAivika. Сразу приведу соответствующую модели диаграмму на рисунке 2. Так может быть проще отслеживать решение задачи.

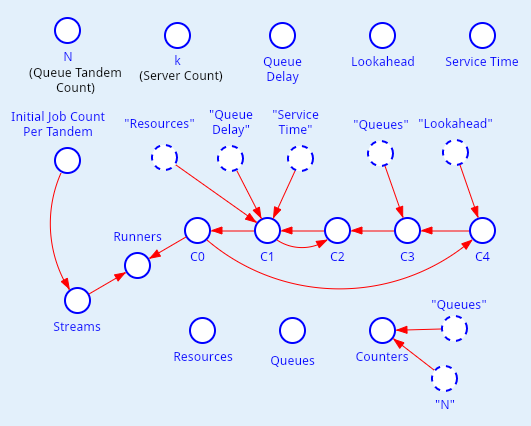
Здесь понадобится версия VisualAivika не ниже 8.0.7. Это важно.

Готовый файл модели можно скачать по следующей ссылке.

Будем моделировать наши серверы как ресурсы прибора. Создадим соответствующий двумерный массив, где первый индекс указывает на тандем, а второй - на номер сервера в тандеме.

Resources = [ Facility.create() | i <- 1..N, j <- 1..k ];

Обработка заявок тандемами начинается с массива C0. Это массив вычислений цепочек блоков. Он имеет следующее определение.

C0 = [ C1[i, 1] | i <- 1..N ];

Здесь мы просто ссылаемся на первый сервер из соответствующего тандема.

Основная обработка идет внутри двумерного массива C1, который имеет более сложное поведение.

C1 = [ Block.seize(Resources[i,j]) >>> 
       Block.advance(exponential(Service_Time)) >>> 
       Block.release(Resources[i,j]) >>> 
       Block.advance(Queue_Delay) >>> 
       C2[i, j] | i <- 1..N, j <- 1..k ];

Здесь мы захватываем сервер, имитируем обслуживание, затем освобождаем сервер и добавляем задержку, которая может означать доставку заявки до следующего пункта обслуживания. Здесь это массив С2.

На самом деле, в VisualAivika нужно вводить такую формулу без отступов и без точки с запятой в конце формулы. На рисунке 3 показано то, как такое выражение выглядит в редакторе уравнений.

Особо нужно отметить, что обработка внутри C1 может быть разной. Например, в примерах к другим своим симуляторам (aivika, DVCompute Simulator, DVCompute++ Simulator) я использовал несколько другое определение массива C1. Это на тот случай, если вы будете сравнивать результаты.

// альтернативное определение из примеров к симуляторам
// aivika, DVCompute Simulator и DVCompute++ Simulator
C1 = [ Block.seize(Resources[i,j]) >>> 
       Block.advance(exponential(Service_Time)) >>> 
       Block.advance(Queue_Delay) >>> 
       Block.release(Resources[i,j]) >>> 
       C2[i, j] | i <- 1..N, j <- 1..k ];

То есть, там прибор отпускался после задержки. Мы же сейчас используем первый вариант, где прибор отпускается до имитации задержки, но после обслуживания.

Рекуррентная формула находится в уравнении для массива C2. Это видно и по приведенной выше диаграмме.

C2 = [ Block.select(if (j == k) 
                    then C3[i] 
                    else Block.transfer(C1[i, 1+j])) | 
           i <- 1..N, j <- 1..k ];

Если второй индекс указывает на последний сервер (прибор) в тандеме, то мы переходим в обработке к массиву C3, а иначе обрабатываем рекурсивно через следующий сервер того же тандема.

Здесь есть тонкий момент. Когда мы ссылаемся на массив С1, то наши индексы должны быть строго в заданных диапазонах 1..N и 1..k, соответственно. Когда второй индекс равен k, то мы попадаем в ветку “then”. Следовательно, индексирование в ветке “else” будет допустимым, если оно происходит динамически. В версии 8.0.7 именно это и происходит. Block.transfer вычисляет свой аргумент динамически. Вычисление аргумента отложенно до момента использования. Поэтому в этой версии такое выражение для вычисления будет корректным.

Вернемся к постановке задачи. Мы хотели считать количество обработанных заявок. Проще всего это cделать с помощью элементов очереди, которые также поместим в массив.

Queues = [ Queue.create() | i <- 1..N ];

Тогда обработка заявок в массиве C3 становится такой, где мы просто регистрируем приход заявок без какой-либо задержки, а потом передаем заявку далее.

С3 = [ Block.queue(Queues[i]) >>> 
       Block.depart(Queues[i]) >>> 
       C4[i] | i <- 1..N ];

Блоки в массиве C4 сначала добавляют задержку по заданному параметру предсказания, а затем случайно выбирают тандем, замыкая всю обработку заявок.

C4 = [ Block.advance(Lookahead) >>> 
       Block.transfer(C0[int(randomInt(1, N))]) | i <- 1..N ];

Функция Block.transfer является особой. Внутри нее можно динамически выбрать новое вычисление для продолжения цепочки блоков. Здесь мы снова возвращаемся к массиву C0, с которого и начали. Распределение - случайное равномерное целочисленное, но нужно еще вызвать функцию int для получения значения индекса.

После определения блоков вычислений нам теперь понадобятся исходные потоки заявок. В этом примере заявки создаются только в начале имитации. Поэтому их количество строго ограничено. За начальные заявки будет отвечать следующий массив, где индексирование идет по количеству тандемов.

Streams =
    [ Stream.take(Stream.randomInt(0, 0), 
          Initial_Job_Count_Per_Tandem) | i <- 1..N ];

Использованный прием позволяет создать заданное количество заявок в начале имитации. Берем бесконечный поток, а потом его ограничиваем.

Чтобы запустить обработку, используем оператор do!, тоже в рамках массива.

Runners = [ do! Block.runByStream(Streams[i], C0[i]) | i <- 1..N ];

Нас интересует количество обработанных заявок. Заявки мы регистрировали в очереди. Поэтому теперь можем запросить такое количество.

Counters = [ Queue.enqueueCount(Queues[i]) | i <- 1..N ];

Осталось определить параметры задачи. Возьмем начальные значения согласно постановке.

N = 4;
k = 50;

Queue_Delay = 1.0;
Service_Time = 10.0;
Initial_Job_Count_Per_Tandem = 60;
Lookahead = 100;

Пусть начальное время имитации равно 0, а конечное - тысячи пятистам (1500). Шаг интегрирования здесь на саму имитацию не влияет, но сильно влияет на отображение графиков. Возьмем условный шаг интегрирования равным 0.25.

Ниже приводятся результаты для эксперимента по методу Монте-Карло для 1000 (тысячи) запусков, но для начала я рекомендую поставить хотя бы 10 запусков.

Результаты приведены на рисунках 4, 5 и 6 ниже. На самом деле, у этих рисунков есть один подвох. Какой именно - читайте далее.

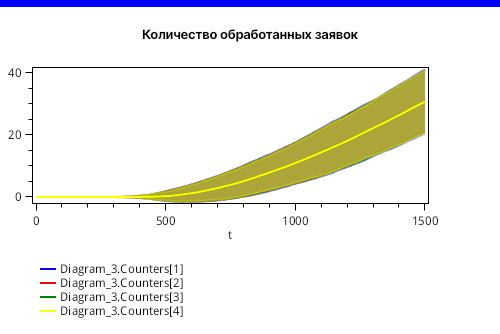
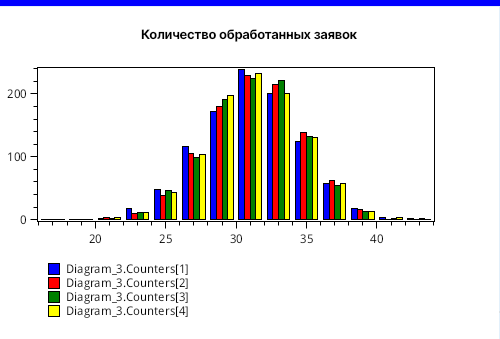
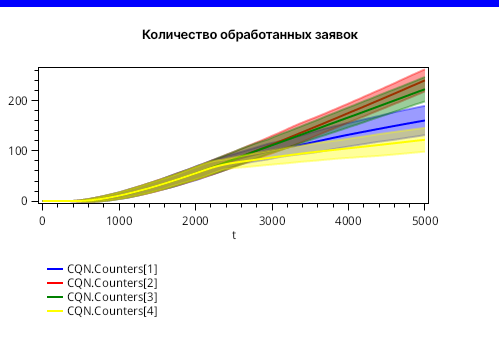
Подвох заключается в том, что при таком конечном времени замкнутость сети не успела отразиться на результатах в полной мере. Если мы увеличим конечное время до 5000, то некоторая равномерность в результатах сохранится, как показано на рисунке 7, хотя в районе 2900 единиц модельного времени едва заметен небольшой перегиб, что, возможно, связано с тем, что все заявки стартуют одновременно.

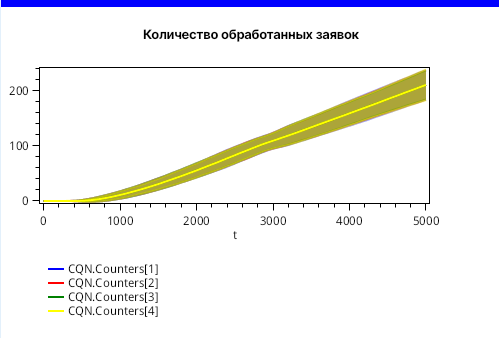
Куда интереснее использовать другое распределение, например, треугольное. Только здесь нужно расширить границы распределения на 0.5 и добавить функцию round (а потом взять минимум и максимум по диапазону индекса, но мы сейчас этого делать не будем).

C4 = [ Block.advance(Lookahead) >>> 
       Block.transfer(C0[int(round(triangular(1-0.499, 2, N+0.499)))]) | i <- 1..N ];

Тогда на рисунке 8 мы увидим ожидаемый перекос по количеству обработанных заявок для нашего приближения треугольного распределения с медианой на тандеме с индексом 2.

Здесь хорошо видно, что второй и третий тандемы обрабатывают заметно больше заявок. Если увеличить количество тандемов N, то рисунок будет красивее и станет отдаленно напоминать спектр.

В общем, этот пример демонстрирует, как можно с помощью массивов определять достаточно нетривиальные системы СМО в VisualAivika.