Моделирование ограниченной очереди в VisualAivika

Автор: Давид Сорокин

Дата публикации: 6 августа 2025 года

В этой статье я собираюсь показать, как моделировать в VisualAivika очереди ограниченной ёмкости. Такая задача может часто встречаться при моделировании систем массового обслуживания (СМО). Помимо этого, VisualAivika поддерживает и системную динамику, в рамках которой можно интегрировать системы обыкновенных дифференциальных уравнений (ОДУ). Более того, системы ОДУ и системы СМО можно комбинировать в рамках одной модели. Однако сейчас речь пойдет об одной задаче — как моделировать очереди ограниченной ёмкости.

Представим себе следующую задачу. По компьютерной сети устройству приходят пакеты в случайном порядке. Допустим, что задержка пакетов имеет показательное распределение со средним 5 единиц модельного времени. Устройство имеет очередь ограниченной ёмкости, скажем, в 7 единиц. Если очередь заполнена, то пакет теряется. Внутри устройства пакеты обрабатываются друг за другом. Время обработки одного пакета имеет равномерное целочисленное распределение в пределах от 0 до 6 единиц модельного времени. Нужно оценить количество потерянных пакетов через 10000 единиц модельного времени.

Итак, у нас есть поток входящих пакетов. В VisualAivika это будет поток внешних событий, где задержка между приходом событий подчиняется некоторому случайному распределению. По условиям задачи задержка имеет показательное распределение со средним 5 единиц.

Packets = Stream.exponential(5);

Мы считаем, что при обработке пакетов есть предельная ёмкость очереди, которую зададим как внешний параметр.

Capacity = 7;

Для блокировки обработки пакетов нам понадобится ресурс, который может обрабатывать не более одного пакета за раз. Такой вид ресурсов называется еще прибором.

Resource = Facility.create();

Для ограничения ёмкости будем учитывать статистику по пакетам, находящимся в очереди ресурса на обработку. При обработке заявок (транзактов) эта статистика будет обновляться автоматически. Тогда мы сможем запросить фактическую длину очереди через вызов функции Facility.queueLength(Resource).

Нам, конечно, интересно количество отказов. Заведем статистику и для этого. Позднее мы сможем построить графики по такой статистике.

FailingQueue = Queue.create();

Теперь определим обработку пакетов (заявок, транзактов). Входящие заявки будут поступать на блок, который будет решать, а не превышена ли ёмкость ресурса? В зависимости от этого пакеты будут перенаправлены на соответствующие блоки.

Chain1Init =
  Block.select(if Facility.queueLength(Resource) < Capacity
               then Chain2Proceed
               else Chain3Fail);

В редакторе уравнений переносы каретки придется заменить на пробелы, а знаки точки с запятой (в конце) вводить не нужно. На рисунке 1 показано, как это должно выглядеть в редакторе уравнений.

Если ёмкость ресурса позволяет, то ставим пакет в очередь на обработку, где возможна блокировка всей цепочки, пока имитируем активность для обработки пакета. Здесь мы захватываем ресурс, затем имитируем активность, а после освобождаем ресурс для других пакетов.

Chain2Proceed =
  Block.seize(Resource) >>>
  Block.advance(randomInt(0, 6)) >>>    // это задержка
  Block.release(Resource) >>>
  Block.terminate;

Иначе, если ёмкость ресурса заполнена, то считаем, что пакет теряется, но статистику все равно собираем, чтобы потом посмотреть ее на графиках, например, на графике отклонения (тренд + доверительные интервалы).

Chain3Fail =
  Block.queue(FailingQueue) >>>
  Block.depart(FailingQueue) >>>
  Block.terminate;

Теперь у нас есть все, чтобы запустить имитацию модели. Берем поток внешних событий и запускаем их обработку заданной цепочкой блоков.

Runner = do! Block.runByStream(Packets, Chain1Init);

Все введенные элементы можно уместить на одной диаграмме, как показано на рисунке 2. Пусть это будет диграмма под названием Model.

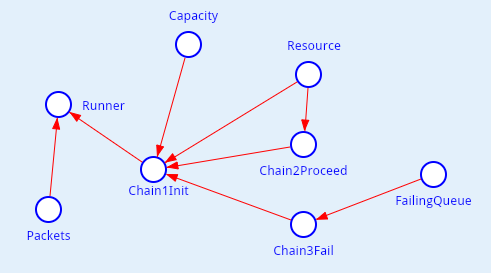
Настало время для вывода графиков. Чтобы в VisualAivika посмотреть их, сначала нужно сформировать показатели. Показатели сами дискретно-событийные, но при переходе на графики и таблицы часть из них немного огрубляется (дискретизируется), но зато это позволяет использовать их в тех же системах обыкновенных дифференциальных уравнений (системная динамика).

Создадим новую диаграмму Results и определим там следующие элементы.

// общее количество отказов
FailCount = Queue.enqueueCount(Model.FailingQueue);

// количество захватов ресурса
CaptureCount = Facility.captureCount(Model.Resource);

// время ожидания в очереди
WaitTime = Facility.waitTime(Model.Resource);

// дискретизированная длина очереди (для ресурса ограниченной ёмкости)
Len = Facility.queueLength(Model.Resource);

// фактическая статистика по длине очереди (для ресурса ограниченной ёмкости)
LenStats = Facility.queueLengthStats(Model.Resource);

Итак, по условию задачи конечное модельное время равно 10000. Ниже в графиках количество экспериментов задано как 1000, но я для начала рекомендую поставить значение 10.

Во-первых, убедимся, что наше ограничение по размеру длины очереди никогда не нарушается. Сначала выведем сводную статистику по длине очереди. Если показатель Len дискретизированный от величины длины очереди “в моменте модельного времени”, то показатель LenStats несет в себе информацию о фактических экстремумах. Ниже на рисунке 4 мы видим, что фактический верхний экстремум никогда не превышает значения, которое было задано в условиях задачи.

В нашем примере процесс быстро становится стационарным. Поэтому ожидаемо, что оба приведенных показателя длины очереди (дискретизированная величина “в моменте” и фактическая статистика по истории наблюдений) сходятся на графике отклонения, который показывает тренды и доверительные интервалы по правилу 3-сигм.

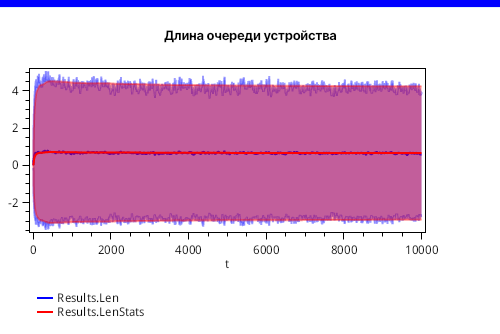
Значит, мы убедились, что инвариант сохранен. Тогда сразу покажем итоговый результат, а потом и остальные показатели, которые могут быть интересны.

График отклонения для числа потерянных пакетов показан на рисунке 5. Отрицательные значения на графике возникают из-за того, что применяется правило 3-сигм, то есть, это значения тренда за вычетом утроенного стандартного отклонения. Эти значения вполне могут быть отрицательными несмотря на то, что сама статистика по значениям неотрицательная.

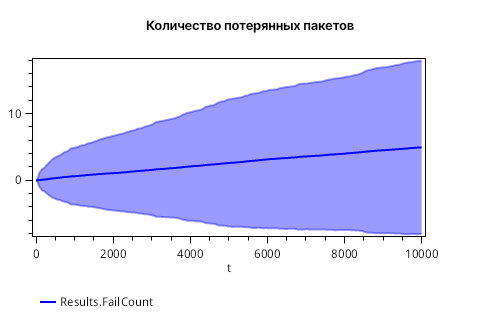
На рисунке 6 ниже можем взгянуть на гистограмму, которая показывает распределение количество потерянных пакетов на момент окончания имитации по всем запускам таких имитаций.

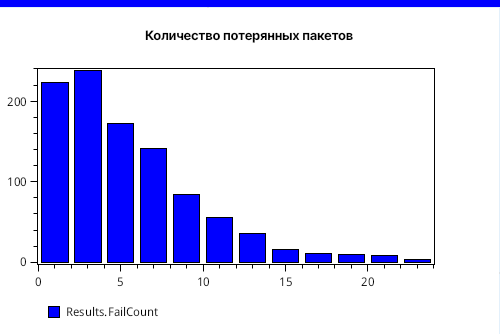
Здесь, кстати, мы видим, что нет отрицательных значений в конечной точке моделирования, о чем мы могли бы подумать, глядя на график отклонения.

Это были ответы на исходную постановку задачи.

Теперь посмотрим на те пакеты, которые все же попали на обработку. Рисунок 7 ниже показывает график отклонения для времени ожидания в очереди для таких пакетов.

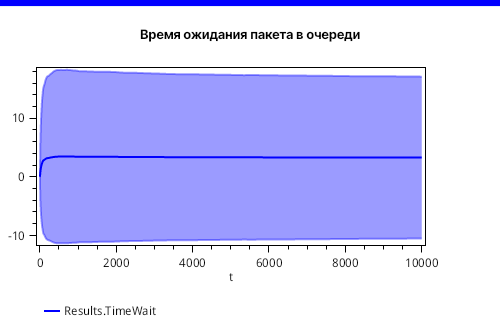
Процесс стал давно стационарным. Поэтому никаких сюрпризов. Более детальная информация по распределению показана на рисунке 8, что отображает статистическую сводку по времени ожидания пакетов в очереди на обработку.

Ну, и, конечно, сложно представить ресурс прибора без информации о том, сколько раз такой прибор был захвачен, в данном случае, обрабатываемыми пакетами. Рисунок 9 дает такую информацию на графике отклонения, где видим восходящий тренд.

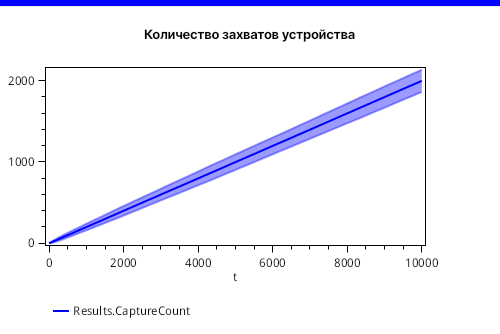
Случайные эффекты накладываются друг на друга, что в итоге дает нормальное распределение для количества захватов в конечной точке моделирования, что наглядно демонстрирует рисунок 10.

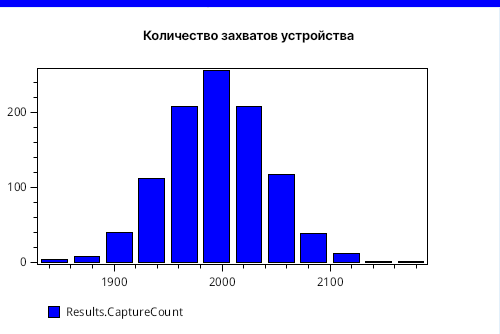
Итого мы взяли модель ограниченной очереди, запустили имитацию и получили ряд интересных графиков и таблиц.